How To Calculate Standard Deviation With Mean And Sample Size

Formula to Calculate Sample Standard Deviation

Sample standard deviation refers to the statistical metric that is used to measure the extent by which a random variable diverges from the hateful of the sample and it is calculated past calculation the squares of the deviation of each variable from the mean Mean refers to the mathematical average calculated for two or more values. There are primarily two ways: arithmetic mean, where all the numbers are added and divided past their weight, and in geometric hateful, nosotros multiply the numbers together, take the Nth root and subtract it with i. read more , then divide the consequence by a number of variables minus and then computing the foursquare root in excel The Square Root function is an arithmetic function built into Excel that is used to make up one's mind the foursquare root of a given number. To use this function, type the term =SQRT and hit the tab central, which will bring up the SQRT function. Moreover, this role accepts a single argument. read more of the result.

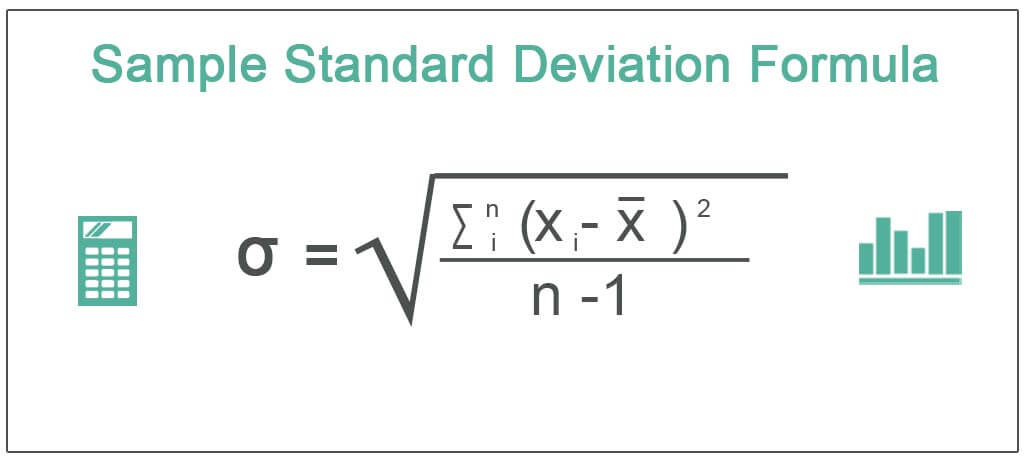
Mathematically, information technology is represented equally,

σ = √ ∑_i ^northward (xi – 10)^two / (north-one)

You are gratuitous to use this image on your website, templates etc, Please provide us with an attribution link Article Link to exist Hyperlinked
For eg:
Source: Sample Standard Deviation Formula (wallstreetmojo.com)

where

x_i = i^th random variable
Ten = Mean of the sample
n = number of variables in the sample

Calculation of Sample Standard Deviation (Pace by Pace)

Lets commencement.

Firstly, gather random variables from a population of a large number of variables. These variables will course a sample. The variables are denoted past ten_i.
Next, determine the number of variables in the sample, and it is denoted by n.
Next, determine the mean of the sample past adding all the random variables and dividing the effect by the number of variables in the sample. The sample mean is denoted by x.
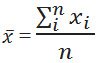
Next, compute the difference betwixt each variable of the sample and the sample mean, i.e., ten_i – x.
Next, calculate the square of all the deviations, i.eastward. (x_i – x)ⁱⁱ.
Next, add all the of the squared deviations, i.e. ∑ (10_i – x)ⁱⁱ.
Next, divide the summation of all the squared deviations past the number of variables in the sample minus ane, i.due east. (n – 1).
Finally, the formula for sample standard deviation is calculated by calculating the square root of the in a higher place-mentioned effect, as shown beneath.

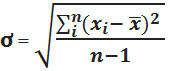
Examples

You can download this Sample Standard Deviation Formula Excel Template here – Sample Standard Deviation Formula Excel Template

Case #one

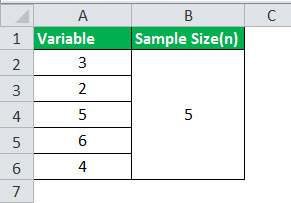
Let us have the example of a sample of 5 students who were surveyed to come across how many pencils they were using every week. Calculate the sample standard deviation of based on their given responses: three, ii, five, 6, 4

Given,

Sample size (north) = 5

Below is given data for the calculation of sample standard deviation.

Sample Mean

Calculation of Sample hateful

Sample hateful = (three + 2 + 5 + 6 + iv) / 5

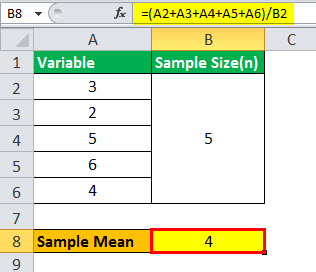
Sample Mean = four

The squares of the deviations of each variable can be calculated as below,

(3 – 4)² = ane
(2 – 4)² = 4
(5 – four)² = ane
(6 – 4)² = 4
(iv – 4)² = 0

At present, the sample standard difference can be calculated by using the above formula as,

ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 – 1)}

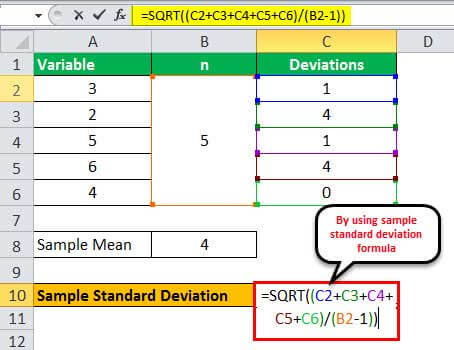
Departure will be –

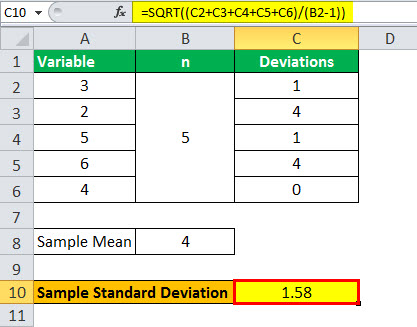
Sample Standard deviation formula example1.3jpg

ơ = 1.58

Therefore, the sample standard deviation is 1.58.

Example #ii

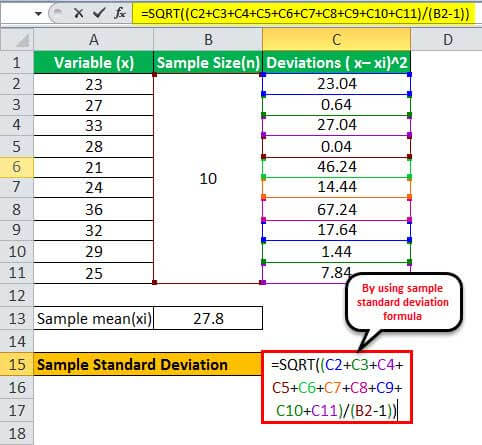
Let united states have the instance of an office in New York where around 5,000 people work and a survey has been carried out on a sample of ten people to make up one's mind the average age of the working population. Determine the sample standard deviation based on the ages of the 10 people given: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25

Given,

Sample size(n) = x

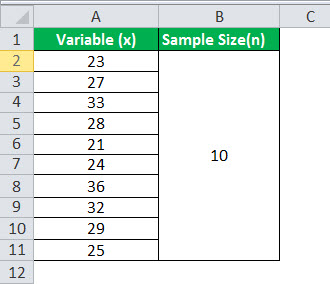
Sample Standard deviation formula example2

By using the above information nosotros will showtime calculate the sample mean

Sample Mean

Calculation of Sample Mean

= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / x

Sample Standard deviation formula example2.1

Sample Mean = 27.8

The squares of the deviations of each variable tin can be calculated equally below,

(23 – 27.eight)² = 23.04
(27 – 27.viii)² = 0.64
(33 – 27.8)² = 27.04
(28 – 27.8)² = 0.04
(21 – 27.viii)² = 46.24
(24 – 27.8)² = xiv.44
(36 – 27.viii)ⁱⁱ = 67.24
(32 – 27.8)ⁱⁱ = 17.64
(29 – 27.eight)² = 1.44
(25 – 27.viii)ⁱⁱ = 7.84

Difference

Now, the deviation can be calculated by using the above formula every bit,

ơ = √ {(23.04 + 0.64 + 27.04 + 0.04 + 46.24 +14.44 +67.24 + 17.64 + 1.44 + 7.84) / (10 – 1)}

Divergence volition exist –

Sample Standard deviation formula example2.3jpg

ơ = iv.78

You can refer to the given excel canvas to a higher place to understand the detailed calculation.

Relevance and Uses

The concept of sample standard difference is very important from the perspective of a statistician because commonly, a sample of data is taken from a pool of large variables (population) from which the statistician is expected to gauge or generalize the results for the entire population. The measure of standard deviation is no exception to this, and hence, the statistician has to make an cess of the population standard departure on the basis of the sample fatigued, and that is where such deviation comes into play.